NumPy features in short

What is NumPy?

NumPy is a python library which provide fixed size multidimensional arrays at creation and functionalities for scientific calculations on those nd-arrays which includes logical,algebrical,mathematical,statistical operations and many more cool features. These are quite different python lists and to keep up with the new python-based software there is a need to understand numpy and have a hands-on numpy.

Now, we are aware of why we use numpy. Let’s jump into some basics of numpy.

Creating an ndarray is the first thing we want to learn

Now, We know how to create an ndarray. It’s time to play with that a bit

let us import numpy as np (for the rest of the tutorial)

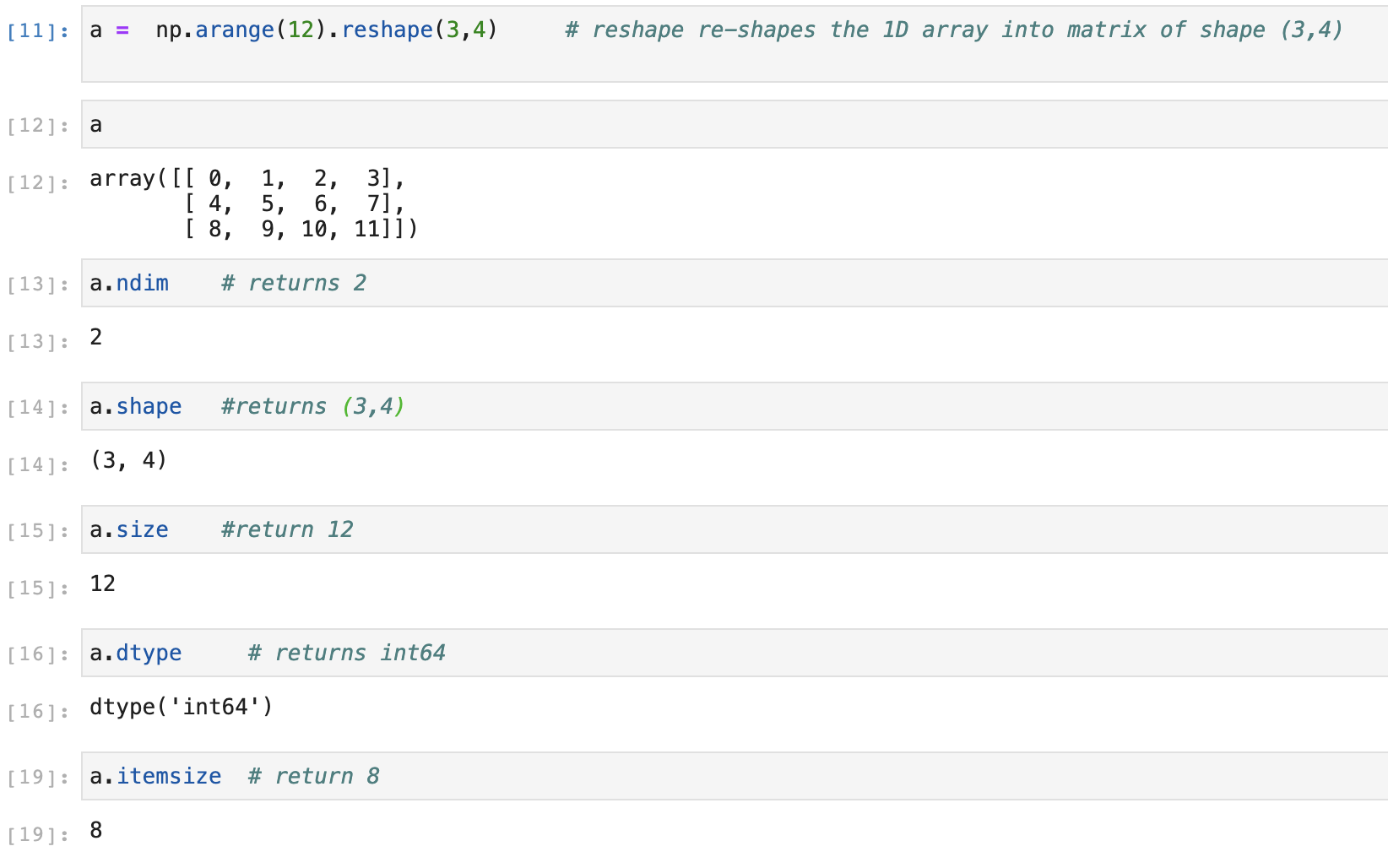
Basics properties of ndarray

* ndim: Gives the number of dimensions(axis)

* shape: gives the shape of the ndarray

* size: gives the number of entries in the ndarray(i.e product of elements in shape)

* dtype: gives the type of array

* itemsize: gives the size of the datatype

Now, Let’s see some other functionalities to initilaize nd-arrays with some custom initializations

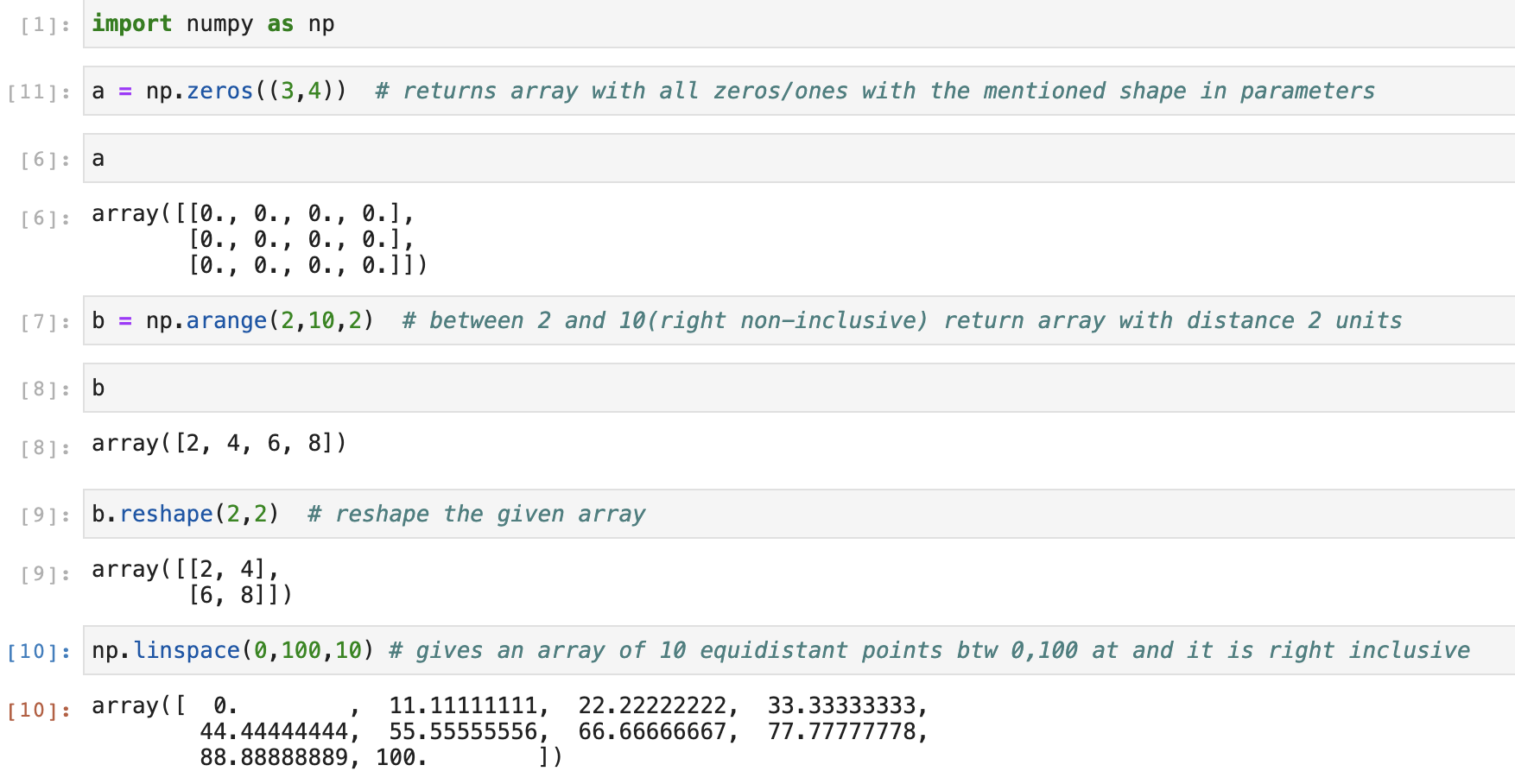
* np.zeros((m,n)): gives a matrix of size mxn with all zeros

* np.ones((m,n)): gives a matrix of size mxn with all ones

* np.arange(m): gives a list of size m from 0 to m-1

* np.arange(i,f,s): gives a list of elements starting from i and with a step of s

* np.ndarray.reshape(a1,...ai,....an)` : reshapes the already existing ndarray. if any one ai is -1. it's size is deciding based on the size of teh ndarray

* np.linspace(i,f, n)`: gives n points between i and f which are equi-distant

Now, Let us code this out in Jupyter Notebook:

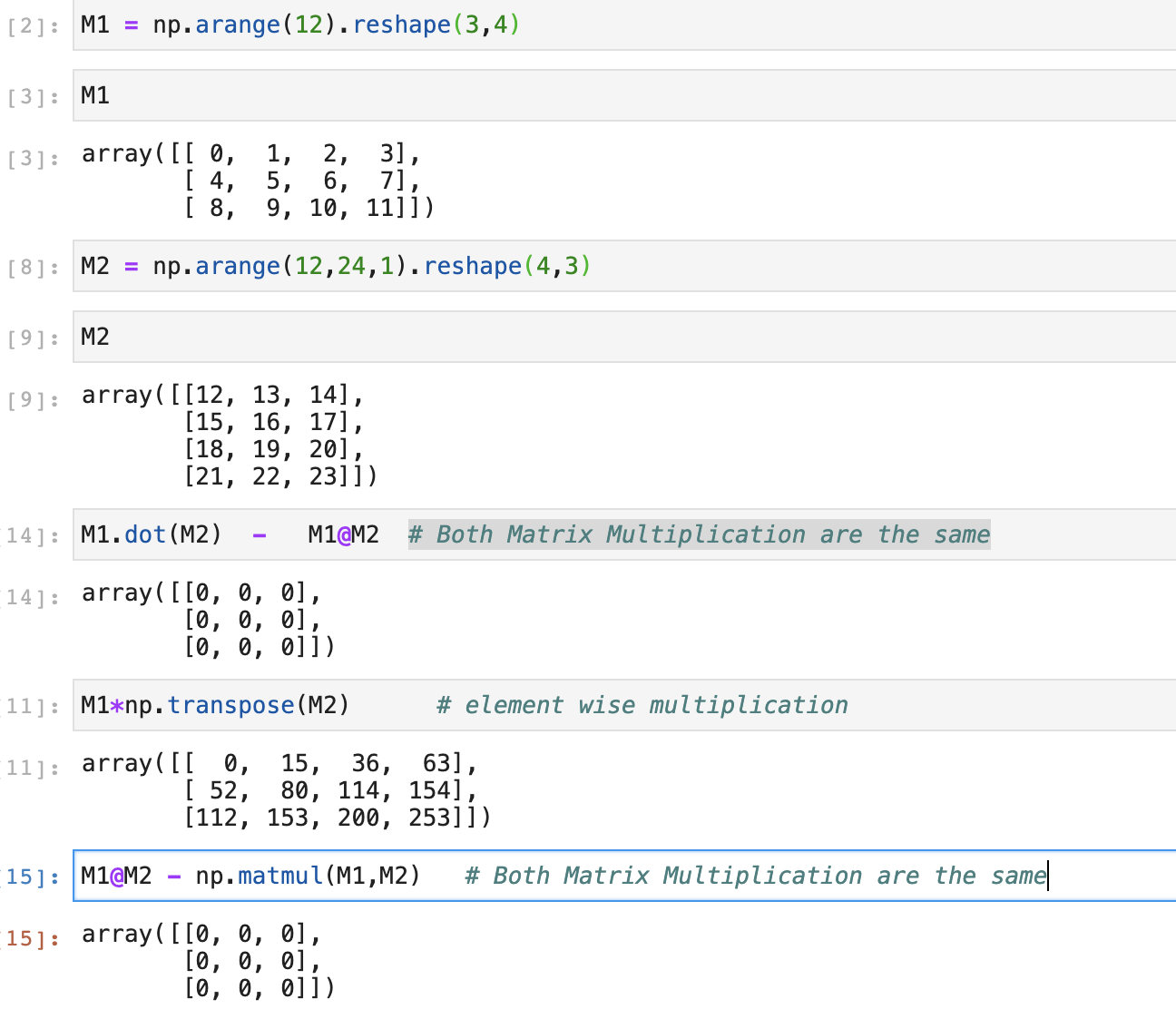
Operations on Matrices

As said earlier numpy provides functionalities for scientific calculations to make life easy for a developer and reduce user written for loops to implement complex multiplications

Now, Let us code this in Jupyter Notebook or some-thing of your choice

Adhoc Properties

>>>a                      # assume a.shape is (2,3)
array([[0.82770259, 0.40919914, 0.54959369],
       [0.02755911, 0.75351311, 0.53814331]])
>>> a.sum()               #returns sum of all the elements in a
3.1057109529998157
>>> a.min()               #return minimum of all the elements in a
0.027559113243068367
>>> a.max()               #return maximum of all the elements in a
0.8277025938204418

when argument like axis = 0 or 1 is mentioned then the arrays collapses along the mentioned axis and the operation happens along the mentioned axis

Example:

>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> b.sum(axis=0)                            
array([12, 15, 18, 21])

Math functions

np.sqrt:return the square root matrix of the given matrix

np.exp(): return the exponential matrix of the given matrix

For Loop

for row in b:
	print(row)  # prints every row


for element in b.flat:
	print(element)     #flattens out the ndarray



a.ravel()              #flattens out the ndarray

a.T                    #returns transpose of a matrix	

a.resize(m,n)          #returns the resized matrix and happens in-place

Stacking

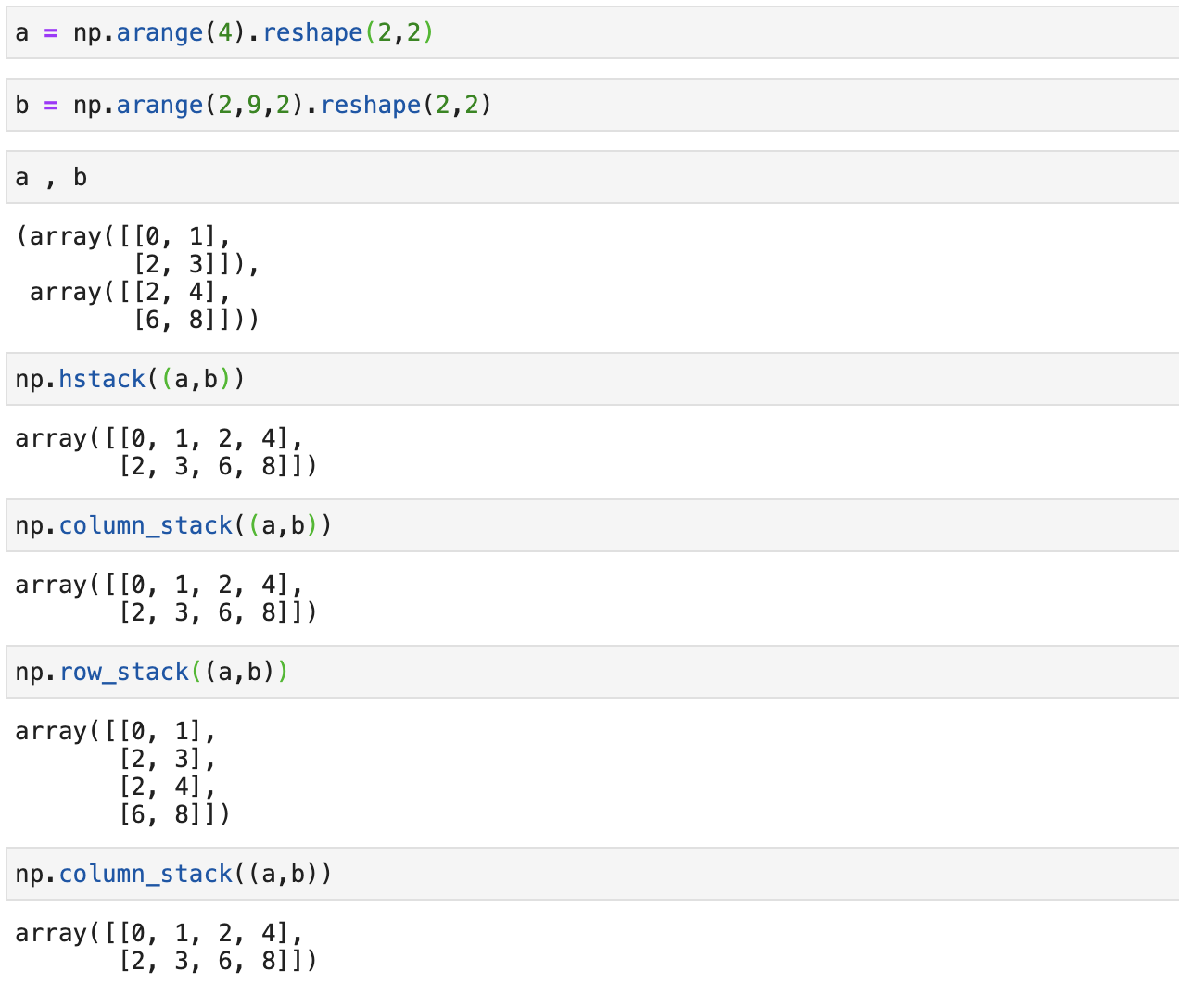
Stacking is a process where we stack up two matrices one on the top of the other or one beside the other

with vstack, arrays are concatenated along axis 0

with hstack, arrays are concatenated along axis 1

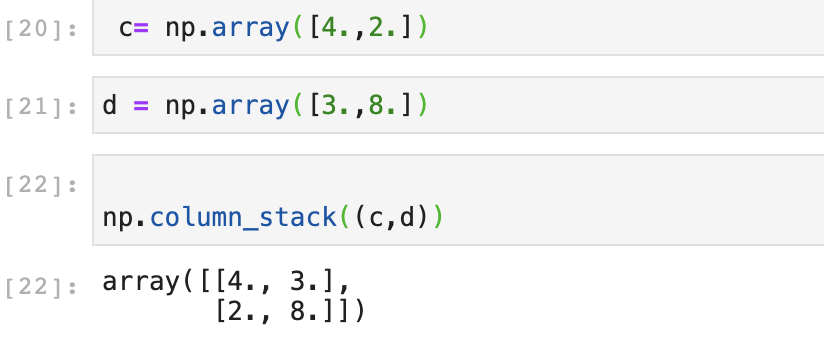
The function column_stack, stacks 1D arrays as columns into a 2D array. It is equivalent to hstack only for 2D arrays

The function row_stack stacks similar to as vstack

Split function

np.hsplit(a,(3,4)): returns arrays split at columns 3,4 resulting into 3 arrays

Making Copies and Deep copy

Storing values in different forms is key to improve the perfomance. Numpy provides us with some ways to make copies and store data.

Simple assignments make no copy of objects

c = a.view() # c is a view of data owned by a i.e  c.flags.owndata return False

Slicing an array returns a view of it

d = a.copy()      #creates a mew ndarray same as a

this is helpful When we need some section of very huge data. we take a copy of that specific data and delete the big-data

Linear Algebra

Here are some of the basic Linear Algebraic functionalities like Transpose, Inverse, Identity , Solving a matrix or finding trace or finding the eigen values and corresponding eigen values. These functions provided in Numpy helps in making the code readable and consistent

a.transpose() # returns transpose of a matrix

np.linalg.inv(a)  # returns inverse of a matrix

np.eye(n)         #returns an identity matrix of size nxn

np.trace(a)       #returns the trace of matrix

np.linalg.solve(a, y)  # solves for x in the expression ax=y

`np.linalg.eig(j)       #  I am yet to explore this `

Here is how we define a function and implement:

import numpy as np 

c = np.arange(12).reshape(3,4)

def softmax(vector):
	e = np.exp(vector)
	return e/e.sum()


def attention(Q,K,V):
	x = np.matmul(Q , np.transpose(K))/np.sqrt(K.ndim)
	sm = np.matmul(softmax(x) , V)
	return sm

print(attention(c,c,c))